Career and background

See also:

Official citation for the 2007 Hans Freudenthal ICMI Award

Introduction: Why different ways of talking about learning and mathematics?

Great many stories of mathematics learning have been told, and they may sometimes be seen as competing with each other. While each one of us may favor one of these stories and call it “the best”, there is no single version that can count as the story of mathematics learning – as the one that is superior to all the rest in some absolute way.

The version to be presented in this unit is called commognitive. Explaining this approach will require engaging with the fundamental questions of what is learning, what is mathematics, and what we mean when we put these two words together and speak about learning mathematics. All this will be done in the modules that follow. This brief introductory talk evolves around the preliminary query: Why should we spend our time trying to define things as basic and obvious as learning or mathematics? In response, it is claimed that the way we speak impacts the way we act.

Bibliography

Sfard, A. (2008 ). Puzzling about (mathematical) thinking (Chapter 1). In Thinking as communicating: Human development, the growth of discourses, and mathematizing (pp. 3 -33). Cambridge, UK: Cambridge University Press.

Learning

This module introduces the commognitive definition of learning. To clarify it fully and to explain why it was chosen from among many existing alternatives, the presentation of the definition is preceded by a brief historical account of research on human development.

Ever since its beginnings, the study of human learning has been fueled by the relentless tension between two desires: the researchers’ wish to capture human learning in all its uniqueness and their wish to do it scientifically, whatever this word meant for them at that time. Because of the conflicting nature of these two desires, it was difficult to attend to both of them at the same time. Whenever a story of learning was told that seemed to satisfy one of them, the resulting research would eventually be criticized for the neglect of the other one. The history of these zigzagging attempts is organized in this talk around the widely differing answers given by various schools of thought to the question “If learning means change, what is it that changes when people learn?” The response adopted by the commognitive researcher seems to constitute an effective tool for capturing the uniqueness of human learning, the goal that can now be pursued without compromising the scientific quality of the endeavor.

Bibliograpghy

Sfard, A. (1998). Two metaphors for learning and the dangers of choosing just one. Educational Researcher, 27(2), 4-13.

Sfard, A. (2015). Learning, commognition and mathematics. In D. Scott & E. ‎Hargreaves (Eds.), The Sage Handbook of Learning (pp. 129-138). London: Sage‎.

Mathematics as discourse

In the last module (Module 2) I defined learning as a process of changing an activity and claimed that school learning aims at those activities that have been developed throughout history and are now prevalent in our society.

In this module I focus on the question of “What is the activity that we change when learning mathematics?” The commognitive answer to this query echoes those given by postmodern thinkers such as Foucault, Lyotard, and Rorty. According to this definition, mathematics is a form of discourse, in which we create theories of mathematical objects, MOs.

Here, the term discourse signifies a form of communication made distinct, among others, by its unique keywords, visual mediators, and routines. Theories of MOs are potentially useful stories about MOs that we gradually construct as we apply these discursive tools. After explaining what is meant by story, I specify the characteristics according to which a story can be considered as useful. Having done all this, we are left  with the task of defining what is meant by mathematical object. The clarification of this latter notion will be the aim of Module 4.

For the summary of our recursive process of defining mathematics, see the diagram below.

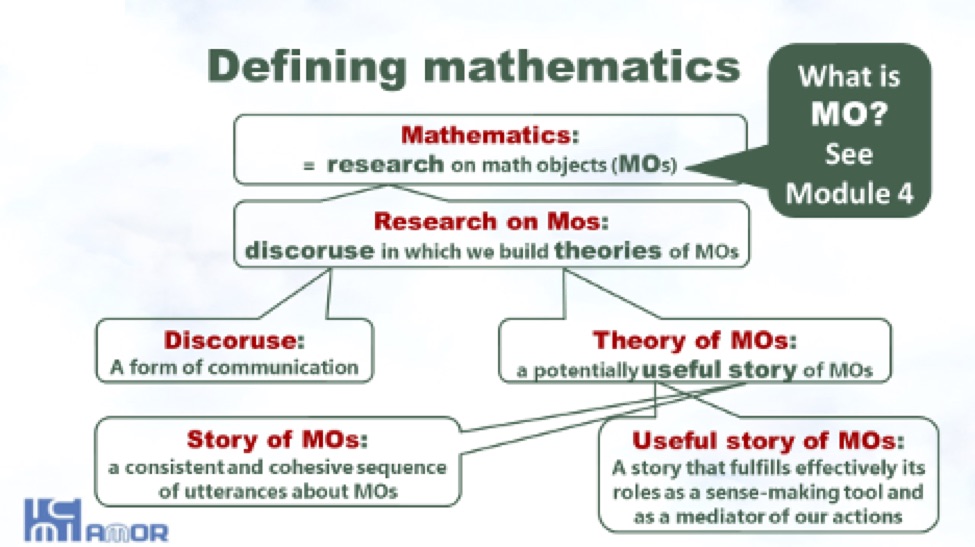
Bibliography

What Is Math? By Dan Falk, Smithonianmag.com, September 23, 2020

What is Mathematics? By Elaine J. Hom LiveScience. com, August 16, 2013 

Sfard, A. (2018). On the Need for Theory of Mathematics Learning and the Promise of ‘Commognition’. In P. Ernest (Ed.), The Philosophy of Mathematics Education Today (pp. 219-228). Cham, Switzerland: Springer.

Defining Mathematical Objects

Having defined mathematics as the activity of telling stories about mathematical objects, I ponder in this module about mathematical objects. These latter entities seem quite unlike those investigated in physics, biology or astronomy. The objects of the scientific discourses, just as those we encounter and talk about in our everyday life, can be experienced directly even before one is able to say anything about them. The case of mathematical objects is quite different. Numbers, functions and derivatives, unlike stones, stars and living creatures, do not wait for us out there to be seen, smelled, heard or felt. If so, what are these objects called mathematical (or MOs, for short), where we can find them and how we can get aware of them and their properties? This two-part module is devoted to all these questions. 

More specifically, in this module I will address the questions of what mathematical objects are and why we need them.

According to the  communitive answer to query 1, mathematical objects are discursive constructs, that is, a special form of speech that allows us to say more in less words. This position contrasts with the classical Platonic view, according to which the entities we talk about in mathematics are of a different ontological status than the talk itself (the latter plays the mere auxiliary role of a medium for describing the preexisting reality).

Bibliography

Sfard, A. (2000). Symbolizing mathematical reality into being: How mathematical discourse and mathematical objects create each other. In P. Cobb, E. Yackel, & K. McClain (Eds.) Symbolizing and communicating: perspectives on mathematical discourse, tools, and instructional design (pp. 37-98). Mahwah, NJ: Lawrence Erlbaum Associates.

Sfard, A. (2008). Chapter 6: Objects of mathematical discourse: What mathematizing is all about. In A. Sfard, Thinking as communicating: Human development, the growth of discourses, and mathematizing. Cambridge, UK: Cambridge University Press.

Developing Mathematical objects

Having described mathematical objects as discursive constructs, that is, as a special form of speech that allows us to say more in less words, I will ask in this module how these constructs come into being. More specifically, a close look will be given to objectification - the process of constructing mathematical objects. This process, its causes and its mechanisms, will be discussed as it occurs on the historical and ontogenetic levels. In both cases, three basic discursive transformations will be identified: those of saming, reifying and encapsulating.  A distinction will be made between primary (unnamed) and discursive objects, and also between concrete and abstract objects. In the end, the question will be asked about the main challenges mathematics students face while faced with the task of constructing a new mathematical object.

Bibliography

Nachlieli, T., & Tabach, M. (2012). Growing mathematical objects in the classroom – the case of function. International Journal of Educational Research, 51-52, 1-27.

Sfard, A. (2015). Metaphors in mathematical thinking and in research on mathematical thinking: a prop or a trap? In F. Caluori, H. Linneweber-Lammerskitten, & C. Streit (Eds.), Beiträge zum Mathematikunterricht (pp. 42-49). Münster: WTM-Verlag.

Defining Routines

Having discussed the first two signature features of mathematical discourses, words and visual mediators – two types of signifiers that yield mathematical objects – I focus in this module on another characteristic of mathematical discoruse, the routines. 
I begin with the question of what routines are. The commognitive definition of routines is followed by a close look at some of their general properties, among them recursivity, interconnectedness, generosy and situativity. A plausible explanation of how we recruit rouitnes in most life situations is derived from the state-od-the-art developments in neuroscience. In the end, a seemingly counterintuitive claim is made: routine moves, rather than being obstacles to the creative action, constitute its vital components.

Bibliography

Lavie, I., Steiner, A., & Sfard, A. (2019). Routines we live by: From ritual to exploration. Educational Studies in Mathematics, 101(2), 153-176. 

Feldman-Barrett, L. (2020). Seven And A Half Lessons About The Brain. New York: Houghton Mifflin Harcourt.

Historical development of mathematics (developing mathematical routines)

Having presented the commognitive vision of mathematics, we return in this module to the original theme to which this series of talks is devoted: the learning of mathematics. This latter activity is now understood as the process of constructing and endorsing ever-new mathematical narratives, which occasionally involves also transforming the discourse in which these stories are told. This definition implies the disappearance of the sharp distinction between learning and the historical development of mathematics – two types of transformations that have been traditionally regarded as ontologically disparate. These two kinds of change are now seen as occurring in the same type of activity, albeit on different planes – individual versus societal (or on different time scales – ontogenetic versus historical). Although they differ in multiple respects, they also share some properties. One of the phenomena that can be observed on both individual and societal planes is that learning may occur in two substantially different ways. The first type of learning, to be called object-level, leads to an expansion of the theory of already existing objects. The other type of development, named meta-level, happens when a new kind of mathematical object is introduced. This time, not just the theory (the collection of endorsed narratives) but the whole discourse may eventually change. The resulting new discourse may be incommensurable with its predecessor, and this means that the endrosability of narratives is now evaluated according to new criteria. The last part of Module 7 is devoted to meta-level societal learning, that is, to historical developments that revolutionize mathematical discourse.  Three questions are addressed: why this kind of learning happens, how it happens, and what makes it possible. The realization that discourses in general, and mathematical discourse in particular, play a critical role in generating and accumulating complexity leads to the conclusion that discourses may bear the main responsibility for human uniqueness.

Bibliography

Sfard, A. (2015). Learning, commognition and mathematics. In D. Scott & E. ‎Hargreaves (Eds.), The Sage Handbook of Learning (pp. 129 - 138). London: Sage‎. 
  
Sfard, A. (2015). Creating numbers: Participationist discourse on mathematics learning. In D. Butlen, I. Bloch, M. Bosch, C. Chambris, G. Cirade, S. Clivaz, S. Gobert, C. Hache, M. Hersant, & C. Mangiante. (Eds.), Rôles et places de la didactique et des didacticiens des mathématiques dans la société et dans le système éducatif. 17è école d'été de didactique des mathématiques. Nantes du 19 au 26 août 2013 (pp. 79 - 98). ‎Grenoble: La pensée sauvage.

Individual Learning (ontogenetic development) of mathematics

n the title of this unit, I promised to tell the commognitive story of mathematics learning. The first six modules had been devoted to constructing the commongnitive discourse. As such, they might have appeared like a mere preparation for the intended endeavor. Then, in module 7, I began actually telling a commognitive story of learning. This time, the focus was on its societal-historical version. In the current module, I complete the picture by doing the same for individual learning. In broad strokes, I present here commognitive ideas about how the newcomer to mathematics may gradually become a full-fledged participant of this historically established discourse. Like in the case of societal learning, I concentrate on meta-level transformations of the discourse. After analyzing the somewhat paradoxical requirements the learner encounters at the entrance to a discourse built around a new mathematical object, I highlight the main mechanisms of the required meta-level learning: the initial construction of the ritualized, process-oriented version of new routines, followed by its gradual transformation into a product-oriented routine. To put it differently, this is the story of the slow emergence of the learner’s personal, tightly knitted network of routines. 
The unit ends here, but the commongnitive story of mathematics learning has by no means been exhausted. By now, you got acquainted with the fundamentals of the commognitive theory of learning, and as they say, nothing is more practical than a well-working theory. Still, to translate the theory of learning into practical advice for those who teach, you must zoom even further into the nitty-gritty of the relevant processes. This unit equipped you with discursive means for the kind of additional work that needs to be done, so you may now try doing this on your own. Before we part, let me say one word about the directions this future storytelling can take. The cornerstone of the theory under construction is the assumption shared by all participationists: individual learning is a collective endeavor. This premise is inscribed in the commognitive tools. To fathom the collective production of success or failure of learning, I would have to consider many factors not yet mentioned in this unit. Except for the most obvious of them, the teaching, it would be necessary to study the role of students’ evolving identities, the shaping impact of culture, the enabling and constraining influences of educational institutions – and the list is still long. In short, the end of this unit is not the end of the storytelling endeavor. While leaving, I hope to return one day with a new season in this commognitive drama of mathematics teaching and learning.

Bibliography 
Sfard, A. (Ed.) (2012). Developing mathematical discourse: Some insights from communicational research (Vol. 51 - 52): Elsevier. 
Sfard, A. (2020). Commognition. In S. Lerman (Ed.), Encyclopedia of Mathematics Education (Second ed.): Springer. 
Sfard, A., & Cobb, P. (2022). Research in Mathematics Education: What Can it Teach us about Human Learning? In R. K. Sawyer (Ed.), Cambridge handbook of learning sciences, 3rd Edition (pp. 467-485). Cambridge, UK: Cambridge University Press.